现代资产投资理论,MPT是什么?有什么用?(附2023年最新排行榜前十名单)
现代资产投资理论,MPT是什么?有什么用?(附2023年最新排行榜前十名单):今天这篇文章,跟大家聊聊现代资产投资理论(Modern Portfolio Theory,简称MPT)。现代资产投资理论(MPT)是什么?有用么?非金融背景出身的读者朋友,也不要太……全球排行榜123网(www.meihu5.com)小编为你整理了本篇文章,希望能解对你有所帮助!
今天这篇文章,跟大家聊聊现代资产投资理论(Modern Portfolio Theory,简称MPT)。现代资产投资理论(MPT)是什么?有用么?
非金融背景出身的读者朋友,也不要太紧张。在这篇文章中,我会尽量用简单平实的语言,跟大家把看似比较专业的金融理论逻辑讲清楚。耐心看完这篇文章,你就会明白,那些看似复杂的金融模型,其实也没那么难以理解。
1952年,哈利·马尔科维奇在《金融杂志》发表了题为《资产组合的选择》的论文,探讨了不同类别的、运动方向各异的证券之间的内在相关性。1959年,马尔科维奇出版了《证券组合选择》一书,详细论述了证券组合的基本原理。该理论,后来被称为现代资产投资理论(MPT)。基于该理论,马尔科维奇后来获得诺贝尔经济学奖。
现代资产投资理论的一大贡献,是在数学上证明了多元分散的价值。对于大多数投资者来说,多元分散,就好像餐桌上摆放着的“免费午餐”。理性的投资者,不应该对它视而不见。
如何来更好的理解这个“免费午餐”呢?在本人主讲的《小乌龟资产配置》网络公开课第二章第六节:多元分散的重要性中,我对这个问题有比较详细的分析。在这里,让我用一个简单的例子帮助大家把其中的逻辑捋一捋。
假设我们购买两支股票。第一支是美国通用电气,另外一支是美国的英特尔。
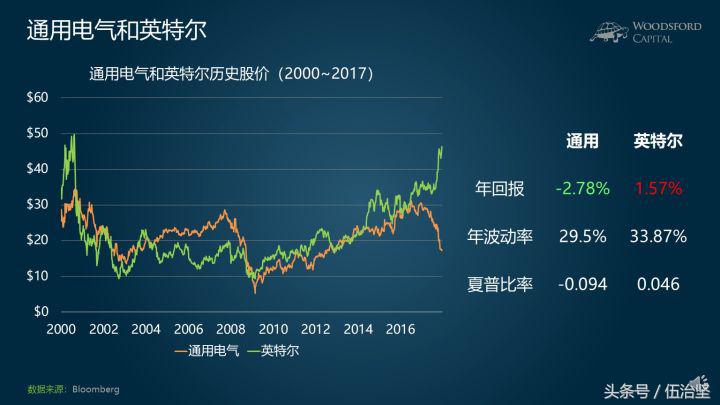
两支股票在过去十几年的股价变化,如图所示。
根据这段股价变化历史,我们可以计算得出,通用电气股票的回报率为每年负2.78%,波动率为每年29.5%,因此夏普比率为负0.094左右(假设无风险利率为0)。同理,英特尔的股票回报率为每年1.57%,波动率为每年33.87%,夏普比率为0.046左右。
所以对于一个投资者来说,如果在十几年前他购买了通用电气,那么很不幸的,他买到了一支“烂股票”。虽然通用电气的名气很响,历史很长,但是作为通用电气的股东,并没有从中获得什么好处。相反,十几年下来,投资回报还是负的。
购买了英特尔股票的股民,其投资回报也好不到哪里去。十几年下来,每年的回报还不到2%。但是相对于通用电气的股东,他们的处境,要稍微好一些。不管是通用还是英特尔,股民都需要承受其股价上下波动带来的不确定性。
这个例子,凸显了股民们面临的窘境:每次选择一个股票购买,他们都承担了一个特殊风险(也被称为非系统风险,Idiosyncratic Risk)。如果股民的运气不好,选错股票,那么他就会蒙受非常大的投资损失。
马尔科维奇的现代资产投资理论指出,通过多元分散,把不同的证券组合起来,投资者可以在不影响投资回报的前提下,有效降低这种非系统风险。
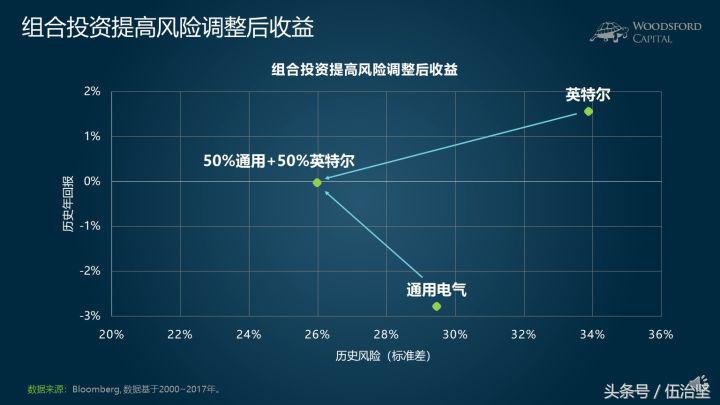
在上面这个例子中,假设我们持有一半的通用电气和一半的英特尔。那么投资者的投资风险(标准差),可以下降到26%左右(如上图),比单独持有通用电气,或者单独持有英特尔股票的风险都要低。
顺着上面的逻辑,如果我们在投资组合中加入越来越多的证券,那么投资者的非系统风险,就会被逐渐降到零(或者非常接近零的低位)。投资者唯一承担的风险,只是系统风险。
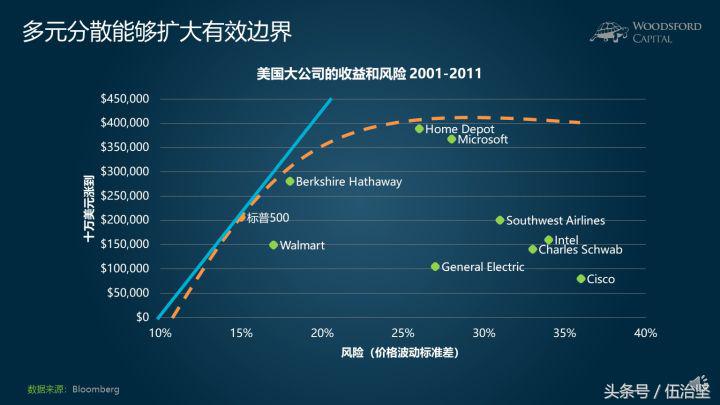
上面这张图,能够帮助我们更好的理解这其中的道理。我们可以看到,标普500指数(目前包含460个美国股票)的风险,比任何一家上市公司的风险都要低。标普500指数的回报,比绝大多数公司(比如沃尔玛、通用电气、英特尔、思科等)的回报都要高。购买标普500指数的投资者,真正获得了“免费午餐”:承担的风险更低,获得的回报更高。
我知道有些朋友可能会说,有几只股票,比如伯克希尔哈撒韦和微软,其回报比标普500指数更高。这个说法没错,但我们也不要忘了以下几点:
首先,像伯克希尔和微软这样的股票,本来就是千里挑一。投资者要选到这样的股票,本身就难度很高。
其次,像伯克希尔和微软这样的公司股票,其风险也要显著高于标普500指数。投资者在微软这样的股票上获得比标普500指数更好的回报,只是因为他承担了更高的投资风险而已,并没有占到什么便宜。
顺着上面的逻辑进一步扩展,在一个多资产的投资组合中,我们把不同的资产类别(前提是它们是能够带来回报的资产,并且各资产价格互相之间的相关性低或者负)组合起来,就能提高投资组合的有效性,在不影响投资组合回报的前提下,降低投资组合的风险。
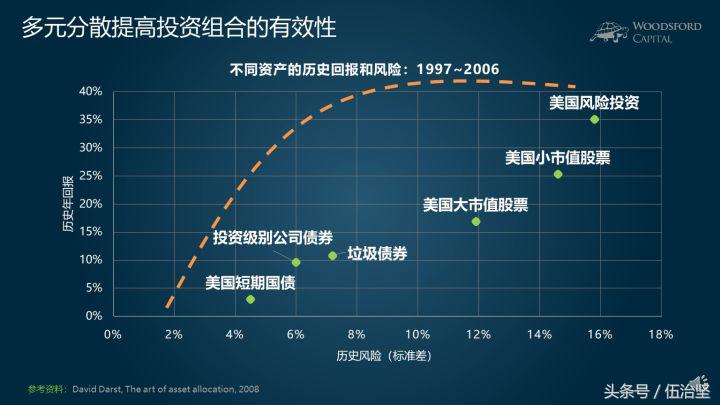
如上图所示,在一个包含国债、公司债券、股票等资产类别的投资组合中,如果给每一个资产类别配备适当的比例,我们就能够找到一个最佳的投资组合(上图中的黄色虚线),帮助投资者达到最佳的风险收益比。
为什么说,黄色虚线上的投资组合,达到了最佳的风险收益比呢?这就涉及到“有效边界”这个非常重要的概念。

假设市场上所有的投资组合,都能够被标示在这张图上。横轴表示的是该投资组合的风险,纵轴表示的是该投资组合的期望回报。每一个不同的投资组合,基于其风险和期望回报,都可以被表示为该图中的一个圆点。
对于投资者来说,如果我们能够在回报不变的情况下降低其风险,即从图中的A点移到B点,那么投资者的效用就得到了提高。或者,在风险不变的情况下,投资组合的回报得到了提高,即从A点移到C点,那么投资者也得到了更高的效用。
在这里,投资组合B和投资组合C,要比投资组合A更好。如果有选择,投资者应该选择B或者C,而不应该持有投资组合A。也就是说,每个投资者都希望尽量找到左上方向的投资组合,可以给他们更高的回报,和更低的风险。
诺贝尔经济学奖得主马尔科维奇,在其提出的现代投资理论中指出,通过多元分散的投资组合,投资者可以优化投资组合的风险调整后收益,将投资者能够投资的有效边界向左上方移动。这个有效边界(上图绿线),就是投资者在充分进行多元分散后,能够达到的最优化,最有效的投资边界。
因此,作为投资者,他的投资目标,应该是找出最佳的资产组合比例,基于该比例达到投资的有效边界。
如何找出这些资产的最佳配置比例,达到投资组合的最佳有效程度呢?这就涉及到另外一个概念:资产组合选择模型(Mean Variance Optimization,简称MVO)。
MVO的意思,是通过大量的统计和数据分析,找出一个投资组合中,各个资产最佳的配置比例,达到上文中所说的有效投资边界。目前在绝大部分大型投资机构中,MVO是使用的最普遍的投资方法之一。该方法的理论基础,就是上文中提到的现代资产投资理论(MPT)。
但是,不管理论有多么漂亮和完美,在现实世界中运用时,总会有这样那样的缺陷。下面,就来说说MVO的缺点。
从上文的解释中,我们应该不难发现,要想找出投资组合的有效边界,关键的前提之一,是确定一项资产(或者证券)的回报和风险。这样,我们才可以把不同的资产以一个个小点的形式,定位在回报~风险的坐标图中。
这里,我们就讲到了MVO中最让人头疼的问题,如何确定一项资产/证券的回报和风险?严格来讲,我们这里说的,是该资产未来的回报(期望回报),和未来的风险(期望风险)。
但是我们都知道,未来是不可预测的。因此绝大部分金融机构的做法,是用过去的历史回报和历史风险(历史波动率),来代替期望回报和风险,并通过模型计算出有效边界。
从统计角度来讲,这样的处理方法给从业人员带来了很多便利。这是因为,如果我们回顾历史,可以找到海量的数据:公司股票的交易历史,可以精确到每天,每小时,甚至每分每秒。其他资产也都有类似的数据可以收集。因此在模型中,我们可以很容易把这些历史数据导入,然后借助计算机算出有效边界。
聪明的读者会发现,用历史数据代替期望值,这种方法管用的关键前提,是未来会重复历史,历史可以预测未来。就是说,一支股票在未来X年的回报,和过去Y年的回报是一样的。其在未来X年的风险(波动率),和过去Y年的风险也是一样的。
如果我们细细想来,在大多数人的投资实践中,确实都是遵从这个假设的:即过去的回报会延续到未来。比如我们去买基金,大部分人都会选过去回报好的,排名靠前的基金,很少有人会反过来,去选那些业绩差的基金。这其中一个关键的隐含条件,就是我们假设过去业绩好的,未来也会好。过去回报差的,未来也会差。
问题在于,这个假设在现实中经不起考验。举例来说,1970~1980年代,全世界表现最好的股市,是日本股市。如果在1990年做一个MVO,那么经过优化的模型,会重仓买入日本股票。而这,恰恰是在最错误的时点,能够做出的最错误的投资决定。
这也是为什么,我们需要向投资者反复强调多元分散的投资原则。背后的原因,除了上文中提到的提高投资组合的有效性,还有一个非常重要的功能,是应对未来的不可知。再复杂和高端的金融模型,也免不了受到各种限制。作为一名理性的投资者,我们需要认识到未来的不可知性,并且在投资实践中,考虑到未来发生我们无法预料的情况的可能性。在任何时候都保持投资组合的多元分散,是应对未来的不可知的必不可少的重要原则。
希望对大家有所帮助。
想要获取更多投资知识和信息的朋友们,可以关注以下渠道:
声明:本文图片、文字、视频等内容来源于互联网,本站无法甄别其准确性,建议谨慎参考,本站不对您因参考本文所带来的任何后果负责!本站尊重并保护知识产权,本文版权归原作者所有,根据《信息网络传播权保护条例》,如果我们转载内容侵犯了您的权利,请及时与我们联系,我们会做删除处理,谢谢。